SLAM-2D实时闭环检测(Real-Time Loop Closure in 2D LIDAR SLAM)

  • SLAM目前是一种实时建立地图的有效方式，实时生成可视化平面图有助于操作者评估捕获数据的质量和覆盖范围。构建便携式捕获平台需要在有限的计算资源下操作。我们介绍了在我们的背包地图平台中使用的方法，它实现了实时地图绘制和5厘米分辨率的环路闭合。为了实现实时闭环检测，我们使用了一种分支定界方法来计算scan-to-submap匹配作为约束，实验证明这个算法比较有竞争力。

I. INTRODUCTION介绍

  • 传统的建图方式是通过CAD(计算机辅助设计)，通过激光卷尺来测量，但是这种方式很慢并且测量人员会先入为主的认为建筑物都是直的，不能很好的描述空间的真实情况。使用SLAM可以迅速而准确地测量大小和复杂程度的建筑物，而手动测量则需要更长数量级的时间。

  • SLAM在这一领域的应用并不是一个新的想法，也不是本文的重点。相反，本文的贡献是一种新的方法，以减少计算回环检测要求的激光距离数据。这种技术使我们能够绘制非常大的楼层，数万平方米，同时为运营商提供充分优化的实时结果。

Scan-to-scan

  • 在基于激光的SLAM方法中，扫描-扫描匹配是计算相对位姿变化的常用方法，但是扫描对扫描匹配本身就会快速累积误差。

    scan-to-scan即为两帧激光扫描之间的匹配

Scan-to-map

  • Scan-to-map的匹配有助于限制这种错误的积累，一个这样的方法，使用高斯-牛顿来寻找线性插值映射上的局部最优值。(Hecktor SLAM) 在对姿态进行良好的初始估计的情况下，通过使用足够高的数据速率的激光雷达，局部优化的扫描到地图匹配是高效和鲁棒的。在不稳定的平台上，利用惯性测量单元(IMU)将激光扇区投影到水平面上，以估计重力方向。

Pixel-accurate scan

  • 像素精确的扫描匹配方法，进一步减少了局部误差积累。尽管计算成本较高，但这种方法也适用于闭环检测。

  • 一些方法通过对激光扫描图像中提取的特征点进行匹配来提高计算成本，其他环路闭合检测方法包括基于直方图的匹配，扫描数据的特征检测，以及使用机器学习。解决剩余局部误差累积的两种常见方法是粒子滤波(Gmaping)和图优化的方法。

  • 粒子滤波器必须在每个粒子中保持完整系统状态的表示。对于基于栅格的SLAM，随着地图变得越来越大，这很快就会占用大量资源。例如：我们的一个测试案例是在3公里的轨道上收集22000平方米的数据。可以用较小维度的特征表示，如不需要每个粒子都有网格地图，可以用来减少资源需求。当需要最新的网格地图时，建议计算子地图，只在必要时更新，以便最终的地图是所有子地图的栅格化。图中的边是由观察产生的约束，可以使用各种优化方法来最小化由所有约束条件引入的误差。例如：这种系统适用于户外基于图的SLAM方法、局部scan-to-scan匹配、基于子地图特征直方图的重叠局部地图匹配等在章节中进行了描述。

III. SYSTEM OVERVIEW

  • 谷歌的SLAM框架Cartographer为室内地图绘制提供了一个实时解决方案，它配备了传感器，可以生成r = 5厘米分辨率的2D网格地图。该系统的操作员可以在穿过建筑物时看到正在创建的地图。激光扫描插入到子图的最佳估计位置，该位置被认为在短时间内足够精确。扫描匹配是针对最近的子映射进行的，所以它只依赖于最近的扫描，并且在世界框架中姿态估计的误差会累积，这使得误差会控制在一定范围之内。

  • 为了在适当的硬件要求下获得良好的性能，我们的SLAM方法不使用粒子滤波器(耗费CPU。为了应对误差的积累，我们定期进行位姿优化。当一个子映射完成时，即不再有新的扫描被插入到它里面，它会参与到回环检测中。所有完成的子映射和扫描都被自动考虑为循环闭合。如果基于当前姿态估计，它们足够接近，扫描匹配器就会尝试在子图中找到扫描结果。如果在当前估计姿态周围的搜索窗口中找到足够好的匹配，则将其作为回环约束添加到图的最佳化问题。通过每隔几秒钟完成一次优化，操作人员的经验是，当重新访问某个位置时，循环会立即关闭。这导致了软实时约束，即闭环扫描匹配必须比添加新的扫描发生得更快，否则它会明显落后。我们通过使用分支定界的方法和每个完成的子映射几个预先计算的网格来实现这一点。

IV. LOCAL 2D SLAM

  • 前端(local slam)和后端优化(global slam)

  • 我们的系统结合了独立的局部和全局方法来实现2D SLAM(对应前后端)。这两种方法都优化了位姿，ξ=(ξx,ξy,ξθ)ξ = (ξx, ξy, ξθ)由一个(x,y)(x, y)平移和一个旋转ξθξθ组成，结合激光雷达观测，这进一步被称为扫描。在不稳定的平台上，例如我们的背包，IMU用于估计重力方向，以便将水平安装的LIDAR扫描投影到2D世界中。在我们的局部方法中，每次连续的扫描都与世界的一小块相匹配，这一小块被称为子地图M(submap)，使用非线性优化将扫描scan与子图submap匹配，这个过程进一步称为扫描匹配。

    惯性测量单元（英文：Inertial measurement unit，简称 IMU）是测量物体三轴姿态角（或角速率）以及加速度的装置。

A. Scans

  • 子地图构建是扫描坐标系与子地图坐标系反复对齐的迭代过程，进一步称为帧。扫描原点为0∈R20∈R^2，我们现在将扫描点的信息写成H={hk}k=1,...,K,hk∈R2H =\{h_k\}_{k= 1,...,K}, h_k∈R^2。扫描帧在子地图中的位姿ξξ表示为变换TξT_ξ，该变换将扫描点刚性地从扫描帧转换为子图帧，定义为:

    \begin{align}T_ξp = \underbrace{\begin{pmatrix}cosξ_\theta & -sinξ_\theta \\ sinξ_\theta & cosξ_\theta\\ \end{pmatrix}}_{R_ξ} p\times\underbrace{ \begin{pmatrix} ξ_x \\ ξ_y\\ \end{pmatrix} }_{t_ξ}& \tag{1}\end{align}

B. Submaps

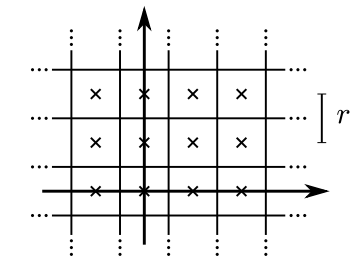
  • 使用几个连续的扫描来构建一个子图，这些子图采用概率网格M的形式：$M:rZ\times rZ\rightarrow [p_{min},p_{max}] $（每个格子的边长就是地图分辨率），子图中离散网格的点之间的距离构成了分辨率r，例如5厘米，成为实际值。这些值可以被认为是一个网格点被阻塞的概率，对于每个网格点，我们定义相应的 pixel 像素，以包含最接近该网格点的所有点。

Fig. 1. Grid points and associated pixels.

  • 无论何时将扫描插入概率网格中，都会计算出命中的网格点集和未命中的网格点集。对于每一次命中，我们将最近的网格点插入命中集合中。对于每一次未命中，我们插入与扫描原点和每个扫描点之间的一条射线相交的每个像素相关联的网格点，不包括已经在命中集合中的网格点。每一个以前没有观察到的网格点在未命中或命中的集合中，则分配一个概率phitp_{hit}或pmissp_{miss}。如果网格点x已经被观察到，我们更新命中和未命中的概率为:

    \begin{align} odds(p) = \frac{p}{1-p}, \tag{2}\end{align}

    \begin{align} M_{new}(x)=clamp(odds^{-1}(odds(M_{old}(x))\cdot odds(p_{hit}))) && \tag{3}\end{align}

    未观察到也是一样的。(在代码中用log来相加表示相乘)

    Fig. 2. A scan and pixels associated with hits (shaded and crossed out) and misses (shaded only).

C. Ceres scan matching 目标匹配器

  • 在将扫描插入子图之前，使用基于Ceresbased[14]扫描匹配器对扫描位姿ξξ值相对于当前的局部子图进行优化。扫描匹配器负责找到一个扫描位姿，使子图中扫描点的概率最大化。我们把它看成一个非线性最小二乘问题：

    \begin{align} argmin \quad \sum_{k=1}^K(1-M_{smooth}(T_ξh_k))^2 &&\tag{CS}\end{align}

    其中 TξT_ξ 根据扫描位姿将 hkh_k 从扫描帧转换为子图。

    函数： Msmooth:R2→RM_{smooth}:R^2 \rightarrow R 是局部子图中概率值的平滑版本。我们使用双三次插值。因此，间隔[0, 1]之外的值可以出现，但被认为是无害的。

    在数学中，双三次插值是三次插值（不要与三次样条插值混淆，一种将三次插值应用于数据集的方法）的扩展，用于在二维规则网格上插值数据点。插值曲面比通过双线性插值或最近邻插值获得的对应曲面更平滑。双三次插值可以使用拉格朗日多项式、三次样条或三次卷积算法来完成。

    在图像处理中，当速度不是问题时，通常在图像重采样中选择双三次插值而不是双线性或最近邻插值。与仅考虑 4 个像素(2×2) 的双线性插值相比，双三次插值考虑 16 个像素 (4×4)。使用双三次插值重采样的图像更平滑，插值伪影更少。

  • 这种光滑函数的数学优化通常比网格的分辨率给出更好的精度。因为这是一个局部优化，所以需要良好的初始估计。可以使用能够测量角速度的IMU来估计各点之间扫描匹配的旋转分量θ。可以在没有IMU的情况下使用更高频率的扫描匹配或像素精确的扫描匹配方法，尽管计算量更大。

V. CLOSING LOOPS

  • 因为扫描只匹配包含几个最近扫描的子图，所以上面描述的方法会慢慢累积错误。对于仅仅几十个连续的扫描，累积的误差是很小的。
  • 更大的空间可以通过创建许多小的子图来处理，我们的方法，优化所有扫描和子地图的位姿，遵循稀疏位姿调整。扫描插入的相对位姿存储在内存中，用于循环闭合优化。除了这些相对位姿，由扫描和子映射组成的所有其他都被认为是一次环路闭合，子图不再改变。扫描匹配器在后台运行，如果出现了匹配良好的结果，则将相应的相对位姿添加到优化问题中。

A. Optimization problem最优化问题

  • 闭环优化，就像扫描匹配一样，也被表述为一个非线性最小二乘问题，可以很容易地添加残差来考虑额外的数据。每隔几秒钟，我们就用Ceres[14]来计算一个解：

    \begin{align} argmin_{ Ξm,Ξs}\quad \frac{1}{2} \sum_{ij}\rho(E^2(\xi_i^m,\xi_j^s;\sum_{ij},\xi_{ij})) \tag{SPA}\end{align}

    子图位姿为Ξm={ξim}i=1,...,mΞ^m = \begin{Bmatrix}ξ_i^m\end{Bmatrix}_{i=1,...,m}和扫描位姿为$ Ξ^s = \begin{Bmatrix}ξ_j^s\end{Bmatrix}{j=1,…,n}在给定约束条件的情况下(坐标变换)进行优化。这些约束以相对姿态在给定约束条件的情况下(坐标变换)进行优化。这些约束以相对姿态ξ{ij}和相关协方差矩阵和相关协方差矩阵Σ_{ij}的形式出现。对于一对子图i和扫描j，位姿的形式出现。对于一对子图 i 和扫描 j ，位姿ξ_{ij}描述了扫描在子映射坐标系中的哪里被匹配。协方差矩阵描述了扫描在子映射坐标系中的哪里被匹配。协方差矩阵Σ_{ij}$可以被评估，例如，遵循[15]中的方法，或局部使用Ceres[14]的协方差估计特征(CS)。该约束的剩余E计算为:

    \begin{align} E^2 (ξ^m_i,ξ^s_j;Σ_{ij},ξ_{ij} ) = e(ξ^m_i,ξ^s_j;ξ_{ij})^T Σ^{−1}_{ij}e(ξ^m_i,ξ^s_j;ξ_{ij}), (4) \end{align}

    \begin{align}e(ξ_i^m,ξ_j^s,ξ_{ij})= ξ_{ij}- \begin{pmatrix} R^{-1}_{ξ_i^m}(t_{ξ_i^m}-t_{ξ_j^s})\\ξ^m_{i;\theta}-ξ^s_{j;\theta}\end{pmatrix}.\tag{5}\end{align}

  • 使用损失函数ρ(降低阈值带来的影响)，例如Huber损失，来减少扫描匹配优化问题中可能出现的（SPA）异常值的影响。例如，这可能发生在局部对称的环境中，如办公室隔间。处理异常值的其他方法包括[16]。

B. Branch-and-bound scan matching 分支定界算法

  • 我们对最佳的像素级别的匹配是感性趣的，W是搜索窗口，MnearestM_{nearest}是将M扩展到R2R^2的所有部分它的参数首先到最近的网格点，即将网格点的值扩展到相应的像素。使用CS可以进一步提高匹配的质量。

    \begin{align}ξ^* = argmax_{ξ\in W} \quad \sum_{k=1}^KM_{nearest}(T_ξh_k),\tag{BBS}\end{align}

  • 通过仔细选择步长来提高效率。我们选择角步长δθδ_θ，使最大扫描距离dmaxd_{max}处的扫描点不超过r，一个像素的宽度。利用余弦定理，我们推导：

    \begin{align}d_{max} = max_{k=1,...,K} ||h_k||,\tag{6}\end{align}

    \begin{align}δ_θ = arccos(1 − \frac{r^2}{2d^2_{max}} ).\tag{7}\end{align}

  • 我们计算一个整数步数覆盖给定的有线性和角度大小的搜索窗口。例如：Wx=Wy=7m,Wθ=30。W_x = W_y = 7m ,W_\theta=30^。

    \begin{align}w_x = \lceil\frac{W_x}{r}\rceil,w_y = \lceil\frac{W_y}{r}\rceil ,w_x = \lceil\frac{W_\theta}{\delta_\theta}\rceil \tag{8}\end{align}

    这导出了一个有限集W，W组成了一个搜索窗口(search window)，它围绕着位于其中心的估计ξ0ξ_0。

    \begin{align}\overline{W} = \begin{Bmatrix} -w_x,...,w_x\end{Bmatrix}\times\begin{Bmatrix} -w_y,...,w_y\end{Bmatrix}\times\begin{Bmatrix} -w_{\theta},...,w_\theta \end{Bmatrix} ,\tag{9}\end{align}

    \begin{align} W = \begin{Bmatrix} ξ_0+(rj_x,rj_y,\delta_\theta j_\theta):(j_x,j_y,j_\theta)\in\overline{W} \end{Bmatrix}. \tag{10}\end{align}

    求ξ∗ξ^*值的朴素算法，可以很容易地表述出来，如算法1描述，但是对于我们想的搜索窗口的大小来说，它将会很慢。

    Algorithm 1 Naive algorithm for (BBS)

    相反，我们采用分支定界法可以在更大的搜索窗口有效地计算ξ值。有关通用方法，请参阅算法2。这种方法首先是在混合整数线性规划问题的背景下提出的[17]。关于这一主题的文献非常广泛;有关简短概述，请参阅[18]。

  • 其主要思想是将可能的子集表示为树中的节点，其中根节点表示所有可能的解，在我们的例子中是W。每个节点的子节点构成其父节点的一个分区，因此它们一起表示相同的可能性集。叶子节点是单例 （singletons）;每一个代表一个可行的解决方案。注意，该算法是精确的。它提供了与单纯方法相同的解决方案，只要内部节点c的得分©是其元素得分的上界。在这种情况下，无论什么时候一个节点是有界的，这个子树中都不存在一个比目前已知的最好的解更好的解。

  • 为了得到一个具体的算法，我们必须决定节点选择、分支和上界计算的方法

1) Node selection

  • 我们的算法使用深度优先搜索(DFS)作为默认选择，在没有更好的选择时: 该算法的效率很大一部分取决于被树的剪支。这取决于两件事:一个好的上界和一个好的当前解决方案。后一部分由DFS帮助，它可以快速地计算许多叶子节点。由于我们不想添加糟糕的匹配作为循环关闭约束，我们还引入了一个分数阈值，低于这个值我们对最优解决方案不感兴趣。由于在实践中通常不会超过阈值，这降低了节点选择或寻找初始 启发式解(initial heuristic solution)的重要性。对于在DFS中访问子节点的顺序，我们计算每个子节点的得分上界，首先访问具有最大边界的最有希望的子节点。该方法为算法3。

2) Node selection

  • 树中的每个节点都由一个整数元组描述c=(cx,cy,cθ,ch)∈Z4.c = (c_x, c_y, c_θ, c_h) ∈ Z^4.高度为ChC_h的节点组合最多2个2Ch×2Ch2^{C_h}\times2^{C_h}可能的转换，但表示一个特定的旋转：

    \begin{align}\overline{\overline{W_c}} = \begin{pmatrix} \begin{Bmatrix} (j_x,j_y)\in Z^2: \begin{cases} c_x \le j_x < c_x + 2^{Ch} \\ c_y \le j_y < c_y + 2^{Ch}\end{cases} \end{Bmatrix} \times \begin{Bmatrix} c_\theta\end{Bmatrix}\end{pmatrix} , \tag{11}\end{align}

    \begin{align} \overline{W_c} = \overline{\overline{W_c}} \cap \overline{W_c}. \tag{12}\end{align}

    Algorithm 2 Generic branch and bound Algorithm 3 DFS branch and bound scan matcher for (BBS)

    树是根据不同分辨率的地图来建立的，高分辨率的地图为上界

    叶节点高度Ch=0C_h = 0，对应可行解ξc∈W,ξc=ξ0+(rcx,rcy，δθcθ).ξc \in W ,ξc = ξ_0 + (rc_x, rc_y， δ_θc_θ).。

  • 在我们的算法3中，包含所有可行解的根节点不明确出现，分支为覆盖搜索窗口的固定高度h0h_0的初始节点集C0C_0

    \begin{align} \overline{W}_{0,x}&= \begin{Bmatrix}-w_x + 2^{h_0}j_x:j_x \in Z,0 \le 2^{h_0}j_x\le 2w_x\end{Bmatrix},\\ \overline{W}_{0,y}&= \begin{Bmatrix}-w_y + 2^{h_0}j_y:j_y \in Z,0 \le 2^{h_0}j_y \le 2w_y\end{Bmatrix},\tag{13}\\ \overline{W}_{0,y} &= \begin{Bmatrix}j_\theta \in Z: -w_\theta \le j_\theta \le w_\theta\end{Bmatrix}, \\C_0 &= \overline{W}_{0,x}\times \overline{W}_{0,y} \times \overline{W}_{0,\theta} \times \begin{Bmatrix} h_0 \end{Bmatrix}.\end{align}

    在具有ch>1c_h> 1的给定节点cc上，我们将其分支为高度ch−1c_h−1的四个子节点

    \begin{align} C_c = ((\begin{Bmatrix}c_x,c_x +2^{c_h-1} \end{Bmatrix} \times \begin{Bmatrix}c_y,c_y + 2^{c_h-1} \end{Bmatrix}\times c_\theta)\cap \overline{W})\times\begin{Bmatrix}c_h - 1\end{Bmatrix}. \tag{14}\end{align}

3) Computing upper bounds

  • 分支定界法的其余部分是计算内部节点上界的一种有效方法，无论在计算量上还是在定界质量上都是如此。我们使用

    \begin{align} score(c) &= \sum_{k=1}^K max_{j \in \overline{\overline{W}}_c } M_{nearest} (T_{ξj}h_k)\\ \tag{15}&\geq \sum_{k=1}^K max_{j \in \overline{W}_c } M_{nearest} (T_{ξj}h_k) \\ &\ge max_{j \in\overline{W}_c }\sum_{k=1}^K M_{nearest} (T_{ξj}h_k)\end{align}

    为了能够有效地计算出最大值，我们使用了预先计算的网格 MprecompCh.M^{Ch}_{precomp}. 对于每个可能的高度chc_h预先计算一个网格，这样我们就可以努力地在扫描点的个数中计算分数。注意，为了能够做到这一点，我们还计算了在搜索空间边界附近大于W‾c\overline{W}_c的最大值$\overline{\overline{W}}_c $。

    \begin{align} score(c) &= \sum_{k=1}^K M_{precomp}^{c_h} (T_{ξc}h_k) \tag{16} \\ \end{align}

    和前面一样，对叶子节点使用ξcξ_c。请注意，MprecomphM_{precomp}^{h}预压缩与MnearestM_{nearest}具有相同的像素结构，但在每个像素中，存储的是从那里开始的2h×2h2^h\times2^h的像素盒的最大值（使格子变粗）。图3给出了这种预先计算网格的一个例子。

    Fig. 3. Precomputed grids of size 1, 4, 16 and 64.

    将64个的栅格值都设置为相同，所以会很占内存

  • 为了降低构造预先计算的网格的计算工作量，我们将等待直到一个概率网格不会收到进一步的更新。然后，我们计算一个预先计算的网格集合，并开始对其进行匹配。对于每个预先计算的网格，我们从每个像素开始计算2h2^h像素宽的行的最大值。使用这个中间结果，然后构造下一个预先计算的网格。

  • 如果值按照添加的顺序被删除，在平摊的O(1)中，可以保持更改的值集合的最大值为最新的。连续极大值保存在deque中，该deque可以递归地定义为包含集合中当前所有值的最大值，然后是在第一个最大值出现后的所有值的连续极大值列表。对于空值集合，此列表为空。使用这种方法，可以在O(n)中计算预计算网格，其中n是每个预计算网格中的像素数。

  • 另一种计算上界的方法是计算较低分辨率概率网格，依次将分辨率减半，参见[1]。由于我们的方法的额外内存消耗是可以接受的，所以我们宁愿使用它而不是使用分辨率较低的概率网格，后者会导致更糟糕的边界(15)从而对绩效产生负面影响。

VI. EXPERIMENTAL RESULTS

  • 在本节中，我们介绍了SLAM算法的一些结果，这些结果来自于记录的传感器数据，使用的是与背包上交互使用的在线算法相同的算法。首先，我们使用位于慕尼黑的德国博物馆(Deutsches Museum)的Cartographer背包中的传感器收集的数据来展示结果。其次，通过使用从机器人吸尘器传感器收集的数据，我们证明了我们的算法在廉价的硬件上工作得很好。最后，我们使用萝卜数据集[19]显示结果，并将自己的结果与已发表的结果进行比较。

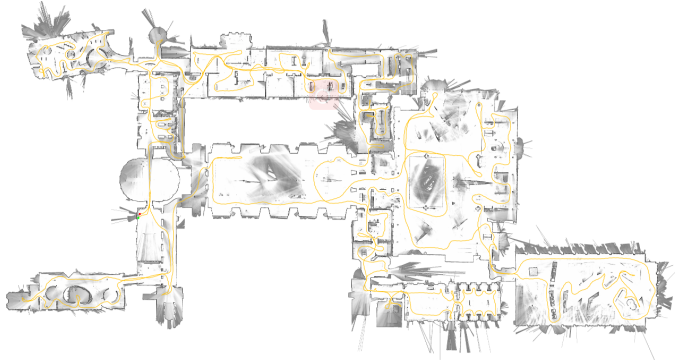
A. Real-World Experiment: Deutsches Museum

  • 利用从德国博物馆收集的数据1,913 s的传感器数据或2,253 m(根据计算解)，我们计算了如图4所示的地图。在使用Intel Xeon E5-1650 3.2 GHz的工作站上，我们的SLAM算法使用了1018秒的CPU时间，使用最多2.2 GB内存，最多4个后台线程用于循环闭合扫描匹配。它在360秒的挂钟时间后结束，这意味着它达到了5.3倍的实时性能。
  • 生成的闭环优化图由11,456个节点和35300条边组成。每次向图中添加几个节点时，都会运行优化问题(SPA)。一个典型的解决方案大约需要3个迭代，并在0.3秒内完成。

Fig. 4. Cartographer map of the 2nd floor of the Deutsches Museum.

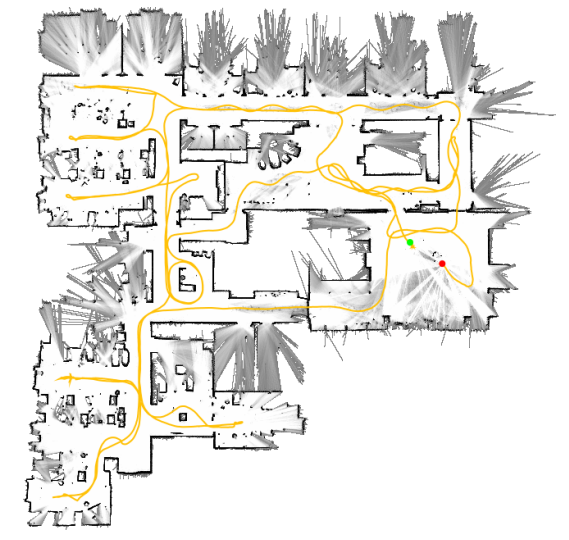
B. Real-World Experiment: Neato’s Revo LDS

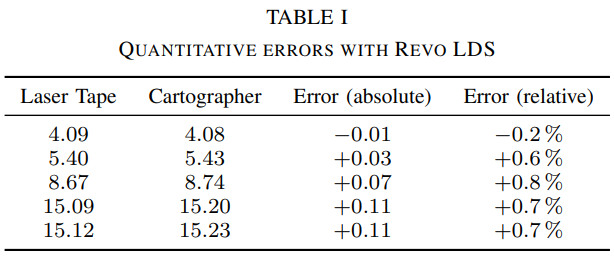
  • 在他们成本低于30美元的真空吸尘器Neato Robotics中使用了一种激光距离传感器(LDS)叫做Revo LDS[20]。我们通过推着手推车上的吸尘器来获取数据，同时在调试连接上以大约2 Hz的频率进行扫描。图5显示了5厘米分辨率的平面图。为了评估平面图的质量，我们将激光卷尺测量的5条直线与绘图工具计算出的结果地图中的像素距离进行了比较。结果如表一所示，所有数值均以米为单位。

    Fig. 5. Cartographer map generated using Revo LDS sensor data.

C. Comparisons using the Radish data set

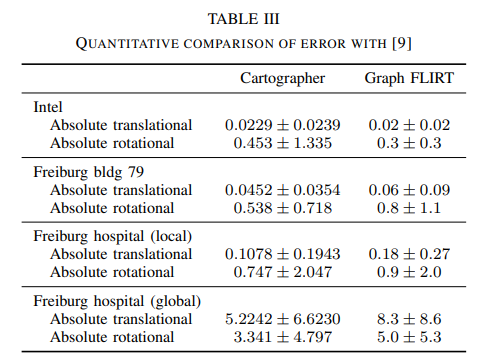
  • 我们使用[21]中提出的基准测量方法将我们的方法与其他方法进行比较，该基准测量方法将相对姿态变化的误差与手动管理的地面真实关系进行比较。表二显示了我们的制图师计算的结果SLAM算法。为了比较，我们引用结果图映射(GM)来自[21]。此外，我们在表III中引用了[9]最近发表的结果。所有的误差都以米和度为单位给出，可以是绝对的，也可以是平方的，以及它们的标准差。

  • 每个公共数据集都是用独特的传感器配置收集的，与我们的Cartographer背包不同。因此，需要调整各种算法参数以产生合理的结果。根据我们的经验，调优制图仪只需要将算法与传感器配置相匹配，而不是与特定的环境相匹配。

  • 由于每个公共数据集都有一个独特的传感器配置，我们不能确定我们的参数是否也适合特定的位置。唯一的例外是Freiburg医院数据集，其中有两个独立的关系文件。我们使用局部关系来调整参数，但也看到了整体关系的良好结果。所有数据集之间最显著的差异是激光扫描的频率和质量，以及里程计的可用性和质量。

  • 尽管公共数据集中使用的传感器硬件相对过时，但Cartographer SLAM的性能始终在我们的预期范围内，即使在MIT CSAIL的情况下我们的性能比Graph Mapping差得多。对于英特尔数据集，我们优于Graph Mapping，但不是Graph FLIRT。在麻省理工学院基利安法庭，我们在所有的指标中的表现优于Graph Mapping。在所有其他情况下，Cartographer 在大多数但不是所有指标上都优于Graph Mapping和Graph FLIRT。

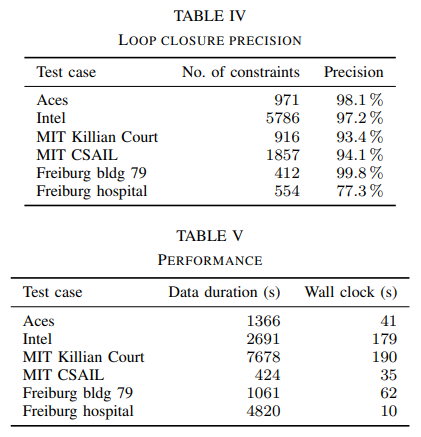
  • 由于我们在子地图和扫描之间添加了循环闭包约束，数据集不包含它们的地面真值。它也很难比较数字与其他基于scan-to-scan的方法。表IV显示了为每个测试用例添加的环路闭合约束的数量(真阳性和假阳性)，以及精度，即真阳性的分数。我们确定真正约束集是所有不违反超过20 cm或1度的闭环约束的子集当我们计算时(SPA)。我们看到，虽然我们的扫描到子映射匹配过程产生了必须在优化(SPA)中处理的误报，但它设法在所有测试用例中提供了足够数量的循环闭包约束。我们对(SPA)中的Huber损失的使用是使循环闭包对异常值具有鲁棒性的因素之一。在弗莱堡医院的案例中，环路闭合检测选择低分辨率和低最低评分会产生相对较高的误报率。通过提高闭环检测的最小分值可以提高精度，但这在某些维度上降低了根据ground truth的求解质量。作者认为，地面真值仍然是最终地图质量的更好基准。

  • 制图者SLAM的参数没有为CPU性能进行调整。我们仍然提供表V中的挂钟时间，这也是在一台Intel Xeon E5-1650的3.2 GHz工作站上测量的。我们提供对传感器数据进行比较的持续时间。

VII. CONCLUSIONS

  • 在本文中，我们提出并实验验证了一个二维SLAM系统，该系统结合了scan-to-submap匹配、闭环检测和图优化。使用我们的局部的、基于网格的SLAM方法，可以创建独立的子地图轨迹。在后台，使用像素精确扫描匹配将所有扫描匹配到附近的子地图，以创建循环闭合约束。在背景中周期性地优化子图和扫描位姿的约束图。该操作符将显示最终地图的最新预览，作为已完成子地图和当前子地图的GPU加速组合。我们证明了在一般的硬件上实时运行我们的算法是可能的。

REFERENCES

  • [1] E. Olson, “M3RSM: Many-to-many multi-resolution scan matching,” in Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), June 2015.

  • [2] K. Konolige, G. Grisetti, R. Kummerle, W. Burgard, B. Limketkai, ¨ and R. Vincent, “Sparse pose adjustment for 2D mapping,” in IROS, Taipei, Taiwan, 10/2010 2010.

  • [3] F. Lu and E. Milios, “Globally consistent range scan alignment for environment mapping,” Autonomous robots, vol. 4, no. 4, pp. 333– 349, 1997.

  • [4] F. Mart´ın, R. Triebel, L. Moreno, and R. Siegwart, “Two different tools for three-dimensional mapping: DE-based scan matching and feature-based loop detection,” Robotica, vol. 32, no. 01, pp. 19–41, 2014.

  • [5] S. Kohlbrecher, J. Meyer, O. von Stryk, and U. Klingauf, “A flexible and scalable SLAM system with full 3D motion estimation,” in Proc. IEEE International Symposium on Safety, Security and Rescue Robotics (SSRR). IEEE, November 2011.

  • [6] M. Himstedt, J. Frost, S. Hellbach, H.-J. Bohme, and E. Maehle, ¨ “Large scale place recognition in 2D LIDAR scans using geometrical landmark relations,” in Intelligent Robots and Systems (IROS 2014), 2014 IEEE/RSJ International Conference on. IEEE, 2014, pp. 5030– 5035.

  • [7] K. Granstrom, T. B. Sch ¨ on, J. I. Nieto, and F. T. Ramos, “Learning to ¨ close loops from range data,” The International Journal of Robotics Research, vol. 30, no. 14, pp. 1728–1754, 2011.

  • [8] G. Grisetti, C. Stachniss, and W. Burgard, “Improving grid-based SLAM with Rao-Blackwellized particle filters by adaptive proposals and selective resampling,” in Robotics and Automation, 2005. ICRA 2005. Proceedings of the 2005 IEEE International Conference on. IEEE, 2005, pp. 2432–2437.

  • [9] G. D. Tipaldi, M. Braun, and K. O. Arras, “FLIRT: Interest regions for 2D range data with applications to robot navigation,” in Experimental Robotics. Springer, 2014, pp. 695–710.

  • [10] J. Strom and E. Olson, “Occupancy grid rasterization in large environments for teams of robots,” in Intelligent Robots and Systems (IROS), 2011 IEEE/RSJ International Conference on. IEEE, 2011, pp. 4271– 4276.

  • [11] R. Kummerle, G. Grisetti, H. Strasdat, K. Konolige, and W. Burgard, ¨ “g2o: A general framework for graph optimization,” in Robotics and Automation (ICRA), 2011 IEEE International Conference on. IEEE, 2011, pp. 3607–3613.

  • [12] L. Carlone, R. Aragues, J. A. Castellanos, and B. Bona, “A fast and accurate approximation for planar pose graph optimization,” The International Journal of Robotics Research, pp. 965–987, 2014.

  • [13] M. Bosse and R. Zlot, “Map matching and data association for largescale two-dimensional laser scan-based SLAM,” The International Journal of Robotics Research, vol. 27, no. 6, pp. 667–691, 2008.

  • [14] S. Agarwal, K. Mierle, and Others, “Ceres solver,” http://ceres-solver. org. [15] E. B. Olson, “Real-time correlative scan matching,” in Robotics and Automation, 2009. ICRA’09. IEEE International Conference on. IEEE, 2009, pp. 4387–4393.

  • [16] P. Agarwal, G. D. Tipaldi, L. Spinello, C. Stachniss, and W. Burgard, “Robust map optimization using dynamic covariance scaling,” in Robotics and Automation (ICRA), 2013 IEEE International Conference on. IEEE, 2013, pp. 62–69.

  • [17] A. H. Land and A. G. Doig, “An automatic method of solving discrete programming problems,” Econometrica, vol. 28, no. 3, pp. 497–520, 1960. [18] J. Clausen, “Branch and bound algorithms-principles and examples,” Department of Computer Science, University of Copenhagen, pp. 1– 30, 1999.

  • [19] A. Howard and N. Roy, “The robotics data set repository (Radish),” 2003. [Online]. Available: http://radish.sourceforge.net/

  • [20] K. Konolige, J. Augenbraun, N. Donaldson, C. Fiebig, and P. Shah, “A low-cost laser distance sensor,” in Robotics and Automation, 2008. ICRA 2008. IEEE International Conference on. IEEE, 2008, pp. 3002–3008.

  • [21] R. Kummerle, B. Steder, C. Dornhege, M. Ruhnke, G. Grisetti, ¨ C. Stachniss, and A. Kleiner, “On measuring the accuracy of SLAM algorithms,” Autonomous Robots, vol. 27, no. 4, pp. 387–407, 2009.