认识整数规划问题
参考文献
什么是线性规划
线性规划概念
-
线性规划(Linear Programming 简记 LP)是了运筹学中数学规划的一个重要分支。自从 1947 年 G. B. Dantzig 提出 求解线性规划的单纯形法以来,线性规划在理论上趋向成熟,在实用中由于计算机能处理成千上万个约束条件和决策变量的线性规划问题之后,线性规划现代管理中经常采用的基本方法之一。 在解决实际问题时,需要把问题归结成一个线性规划数学模型,关键及难点在于选适当的决策变量建立恰当的模型,这直接影响到问题的求解。
-
线性规划问题的目标函数及约束条件均为线性函数;约束条件记为 s.t.(即 subject to)。目标函数可以是求最大值,也可以是求最小值,约束条件的不等号可以 是小于号也可以是大于号。
-
一般线性规划问题的数学标准型为
\begin{align} max \quad z = \sum^n_{j = 1} c_j x_j \tag{3} \end{align}
\begin{align} s.t.\quad \begin{cases} \sum^n_{j = 1}a_{ij}x_{j} = b_i \quad i = 1,2,...,m \\ x_j \ge 0 \quad j=1,2,...,n \tag{4}\end{cases} \end{align}
-
例题
某机床厂生产甲、乙两种机床,每台销售后的利润分别为4000元与3000元。生产甲机床需用A、B机器加工,加工时间分别为每台2小时和1小时;生产乙机床需用A、B、C三种机器加工,加工时间为每台各一小时。若每天可用于加工的机器时数分别为A机器10小时、B机器8小时和C机器7小时,问该厂应生产甲、乙机床各几台,才能使总利润最大?
上述问题的数学模型:
设该厂生产台甲机床和乙机床时总利润最大,则,应满足
\begin{align} max \quad z = 4x_1 +3x_2 \tag{1}\end{align}
\begin{align}s.t. \begin{cases} 2x_1 + x_2 \le 10\\x_1 + x_2 \le 8 \\x_2 \le 7\\ x_1,x_2 \ge 0 \end{cases} \tag{2}\end{align}
-
上述例题中变量称之为决策变量,(1)式被称为问题的目标函数,(2)中的几个不等式是问题的约束条件,记为s.t.(即subject to)。由于上面的目标函数及约束条件为线性函数,故被称为线性规划问题。
线性规划问题的解的概念
- 可行解:满足4个约束条件的解,称为可行解。 而使目标函数达到最大值的可行解叫最优解。
- 可行域:所有可行解构成的集合称为问题的可行域,记为R 。
求线性规划解的方法
-
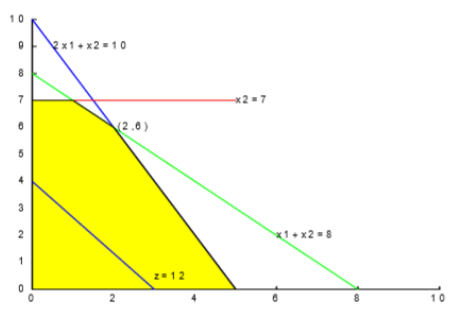
图解法
简单直观,适用于二维决策变量,它有助于了解线性规划问题求解的基本原理。。对于每一固定的值z,使目标函数值等于z的点构成的直线称为目标函数等位线,当z变动时,我们得到一族平行直线。
图解法简单直观,对于每一固定的值z,使目标函数值等于z的点构成的直线称为目标函数等位线,当z变动时,我们得到一族平行直线。等位线向上平移即可找到事目标函数有最大值的点。不难看出最优解为(2,6),带入目标函数即可。
-
单纯形法
当变量变多时,我们不能简单的画出图像,并且为了能够让计算机计算,我们需要借助单纯形法。单纯形法是求解线性规划问题最常用、最有效的算法之一。
这个算法的思想可以用几何术语描述如下:
先在可行域中找到一个极点,然后检查一下是不是在邻接极点除可以让目标函数取值更佳。如果不是,当前顶点就是最优点,然后算法停止;如果是,转而处理那个能让目标函数取值更佳的邻接顶点。有限步以后,该算法要么发现了一个取到最优解的极点,要么证明了最优解不存在。
这个算法的思想可以用几何术语描述如下:
先在可行域中找到一个极点,然后检查一下是不是在邻接极点除可以让目标函数取值更佳。如果不是,当前顶点就是最优点,然后算法停止;如果是,转而处理那个能让目标函数取值更佳的邻接顶点。有限步以后,该算法要么发现了一个取到最优解的极点,要么证明了最优解不存在。
参考《算法设计与分析基础》潘彦译 P267
整数规划是什么
整数规划的分类
-
如不加特殊说明,一般指整数线性规划。对于整数线性规划模型大致可分为两类:
- 变量全限制为整数时,称纯(完全)整数规划。
- 变量部分限制为整数的,称混合整数规划。
整数规划特点
-
原线性规划有优解,当自变量限制为整数后,其整数规划解出现下述情况:
- 原线性规划优解全是整数,则整数规划优解与线性规划优解一致。
- 整数规划无可行解。
- 有可行解(当然就存在优解),但优解值变差。
-
整数规划优解不能按照实数优解简单取整而获得。
-
例题1
原线性规划为:
\begin{align} &min \quad z = x_1 + x_2 \\ &2x_1+4x_2 = 5 ,\quad x_1 \ge 0,x_2\ge0 \end{align}
其最优实数解为: $$ \begin{align} x_1 = 0,x_2 = \frac{5}{4}, minz = \frac{5}{4}\end{align}$$
-
例题2
原线性规划为:
\begin{align} &min \quad z = x_1 + x_2 \\ &2x_1+4x_2 = 6 ,\quad x_1 \ge 0,x_2\ge0 \end{align}
其最优实数解为: $$ \begin{align} x_1 = 0,x_2 = \frac{3}{2}, minz = \frac{3}{2}\end{align}$$
若限制整数得: $$ \begin{align} x_1 = 1,x_2 = 1, minz = 2\end{align}$$
整数规划如何求解
- 分枝定界法—可求纯或混合整数线性规划。
- 割平面法—可求纯或混合整数线性规划。
- 隐枚举法—求解“0-1”整数规划:
- 过滤隐枚举法
- 分枝隐枚举法
- 匈牙利法—解决指派问题(“0-1”规划特殊情形)
- 蒙特卡洛法—求解各种类型规划。