分支定界法如何求解整数规划问题

参考资料

• 整数规划
• （不太了解原由建议先看这个）认识整数规划问题
• 整数规划：分支定界法（有算法实现）
• 分枝定界图解（含 Real-Time Loop Closure in 2D LIDAR SLAM论文部分解读及BB代码部分解读）
• 数学建模–整数规划

分支定界法

​ 分枝定界是一种深度优先的树搜索算法。通过对树进行剪枝，可以缩小了搜索范围，大大减小计算量。但同时又不会遗漏最优解。请现在就记住，分枝定界思想，就是不断缩小搜索范围的过程。

主要思路

• 对有约束条件的优化问题（其可行解为有限数）的所有可行解空间恰当地进行系统搜索，这就是分枝与定界内容。

• 通常，把全部可行解空间反复地分割为越来越小的子集，称为分枝；并且对每个子集内的解集计算一个目标下界（对于最小值问题），这称为定界。在每次分枝后，凡是界限超出已知可行解集目标值的那些子集不再进一步分枝，这样，许多子集可不予考虑，这称剪枝。这就是分枝定界法的主要思路。

• 分枝定界法可用于解纯整数或混合的整数规划问题。在本世纪六十年代初由 Land Doig 和 Dakin 等人提出的。由于这方法灵活且便于用计算机求解，所以现在它已是解整数规划的重要方法。目前已成功地应用于求解生产进度问题、旅行推销员问题、工厂选址问题、背包问题及分配问题等。

举例分析

​ 设有最大化的整数规划问题$A$，与它相应的线性规划为问题$B$，从解问题$B$开始，若其最优解不符合$A$的整数条件，那么$B$的最优目标函数必是$A$的最优目标函数$z^*$的上界,记作$\overline{z}$；而$A$的任意可行解的目标函数值将是$z^*$的一个下界$\underline{z}$。 分支定界法就是将$B$的可行域分成子区域的方法。逐步减小$\overline{z}$和增大$\underline{z}$，最终求到$z^*$。

• 例

  $Max \quad z = 40 x_1 +90x_2$

  \begin{align} s.t. \quad \begin{cases} 9x_1 +7x_2 \le 56\\ 7x_1 + 20x_2 \le 70\\ x_1,x_2 \ge 0,integer \end{cases} \end{align}

  解：

  • 先不考虑整数限制，即解相应的线性规划$B$，得最优解为：

    $x_1 = 4.8092,x_2 = 1.8168,z =355.8779$

    可见她不符合整数条件。这时$z$是问题$A$ 的最优目标函数值$z^*$的上界，记作$\overline{z}$。而$x_1= 0，x_2= 0$显然是问题A的一个整数可行解，这时$z=0$,是$z^*$的一个下界，记作$\underline{z}$,即$ 0\le z^* \le 355$。

  • 因为$x_1,x_2$当前均为非整数，故不满足整数要求，任选一个进行分枝。设选$x_1$进行分枝，把可行集分成2个子集(以下为增加的约束)：

    $x_1 \le [4.8092]=4, \quad x_1 \ge [4.8092] +1 =5$

    因为4与5之间无整数，故这两个子集的整数解必与原可行集合整数解一致。这一步称为分枝。这两个子集的规划及求解如下：

    • 问题$B_1:$

      $Max \quad z = 40x_1 + 90x_2$

      \begin{align} \begin{cases} 9x_1 + 7x_2 \le 56\\7x_1+20x_2 \le70 \\0\le x_1 \le4,x_2\ge0 \end{cases} \end{align}

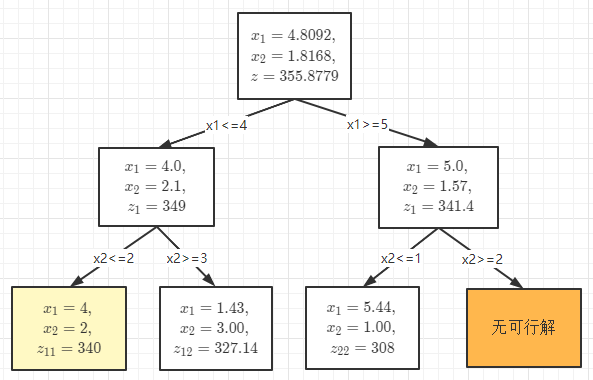
      最优解为: $$ x_1 = 4.0,x_2 =2.1,z_1 =349$$

    • 问题$B_2:$

      $Max \quad z = 40x_1 + 90x_2$

      \begin{align} \begin{cases} 9x_1 + 7x_2 \le 56\\7x_1+20x_2 \le70 \\x_1\ge5,x_2\ge0 \end{cases} \end{align}

      最优解为: $$ x_1 = 5.0,x_2 =1.57,z_1 =341.4$$

    • 再定界：$0 \le z^* \le 349$

  • 对问题$B_1:$再对不是整数的$x_2$进行分枝得问题$B_{11}$和$B_{12}$，它们的最优解为：

    • $B_{11}:x_1 = 4,x_2 = 2,z_{11} = 340$

    • $B_{12}:x_1=1.43,x_2=3.00,z_{12}=327.14$

    • 由开头所说，线性规划$B$的最优目标函数值必是$A$的最优目标函数$z^*$的上界,记作$\overline{z}$，整数规划$A$的任意可行解的目标函数值将是$z^*$的一个下界$\underline{z}$。

    • 再定界有：$340 \le z^*\le349$，并将不在这个范围内的$B_{12}$剪枝。

  • 对问题$B_2$再进行分枝得问题$B_{21}$和$B_{22}$，它们的最优解为：

    • $B_{21}:x_1 = 5.44,x_2 = 1.00,z_{22} = 308$
    • $B_{22}$无可行解
    • 再定界有：$340 \le z^*\le341$将$B_{21},B_{22}$ 剪枝。

  • 于是可以断定原问题的最优解为：

    $x_1 = 4,x_2 = 2,z^{*} = 340$

  • 但是我认为现在还不能断定这个解就是原问题的最优解，刚开始是选择的是x1,我认为可能还需要对x2进行这样的分枝定界才能最终确定最优解是什么，可能理解的不准确仅作参考。

• 图解如下