王树森深度强化学习基础笔记

参考资料

• 王树森教授【深度强化学习完整版】
• 马尔可夫链

基本概念

随机变量Random Variable

• a variable whose values depend on outcomes of a random event.
• 随机变量，表示一个事件所有可能的结果的集合，用大$X$表示，$\mathbb{P}()$表示概率

举例一枚硬币，则有：

$\mathbb{P}(X = 0) = 0.5$

$\mathbb{P}(X = 1) = 0.5$

• 用x表示随机变量$X$的一个观测值，x表示一个数没有随机性

概率密度函数Probability Density Function （PDF）

• PDF provides a relative likelihood that value of the random variable would equal that sample.
• 概率密度函数表示随机变量在某个确定位置的取值点附近的可能性

Example: Gaussian distribution

• It is a continuous distribution.高斯分布

\begin{align}p(x) = \frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{(2-\mu)^2}{2\sigma^2}).\end{align}

• 其中$\mu$表示均值，$\sigma$表示标准差

• 概率密度中，将随机变量$X$的定义域记为$\chi$

• 当p为连续的概率分布

  \begin{align} \int_\chi p(x)dx = 1\end{align}

• 当p为离散的概率分布

  \begin{align} \sum_{x\in\chi} p(x)dx = 1\end{align}

Expectation

• 函数$f(x)$的期望表示为，对其与概率密度函数的乘积做定积分，表示为如下公式:

• 连续性

  \begin{align} \mathbb{E}[f(X)] =\int_\chi p(x)f(x)dx\end{align}

• 离散性

  \begin{align} \mathbb{E}[f(X)] =\sum_{x\in\chi} p(x)f(x)dx\end{align}

Random Sampling

随机抽样

随机抽三个颜色的球，概率分别为0.2，0.5，0.3

form numpy.random import choice 
samples = choice(['R','G','B'],size = 100 ,p = [0.2,0.5,0.3])
print(samples)

Terminology

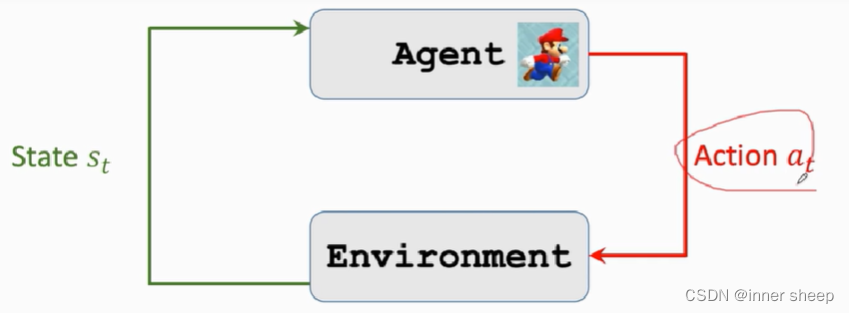
state： s (this frame)，某一时刻的状态

Action：动作，Action a $\in$ {left，right，up}

Agent：代理，也被指为智能体是动作执行者，机器人、智能体

policy：也叫 $\pi$ 函数，根据观测到的状态来做出决策，从而控制agent运动，在数学上是概率密度函数，数学上表示为：

\begin{align} \pi:(s,a)->[0,1]:\pi(a|s) = \mathbb{P}(A =a|S = s). \end{align}

其中a是某一个动作，s表示当前状态，函数的结果为此时的概率

强化学习就是去构建policy函数，只要有了这样一个policy函数，计算机就会根据概率密度得出的概率做随机抽样，进而控制agent做出反应

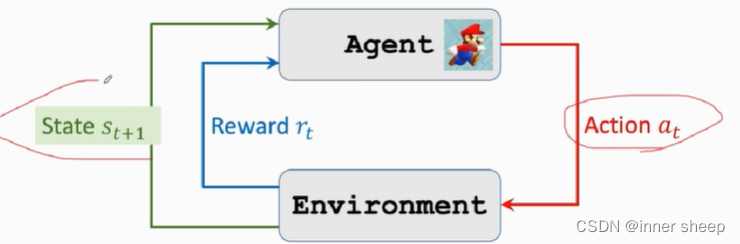
reward： 用R表示，奖励，奖励定义的好坏影响强化学习的结果，奖励的定义是更具游戏中输赢的条件来设置的。强化学习的目标就是获得奖励的总和最高。

state transition：状态转移，状态转移通常具有随机性，符合马尔科夫链模型，状态转移的随机性是更具环境的变化来的，环境的变化对于强化学习是未知的，状态转移函数只有环境知道，用数学公式表示如下：

$p(s'|s,a)=\mathbb{P}(S' = s' | S = s,A =a)$

agent environment interaction

用游戏来举例，环境是游戏程序，agent是游戏角色。在游戏中，将当前屏幕显示的图片作为State $S_t$ ,agent会根据环境做出动作，做出动作之后，环境会更新状态。

agent做出动作之后环境会更新状态，并给agent响应的奖励$r_t$

强化学习的两个随机性：

• agent的动作Action存在随机性
• 状态转移，当agent做出动作后，环境会发生状态转移，具有随机性，环境根据概率密度算出概率，再根据随机抽样得到下一个状态$S'$，数学公式如下：

Play the game using AI

1. 通过强化学习构建出police函数 $\pi$
2. 观测当前游戏的这一帧的状态State,S1，AI用police函数来算出动作action,a1(左，右，上，三选一)
3. 环境生成下一个状态S2，并且给agent对应的奖励reward,r1
4. AI将新的State S2作为输入，用policy函数算出动作action，a2
5. …直到game结束

最终得到trajectory轨迹，包含每一步的[状态，动作，奖励]，行成一个矩阵

Rewards and Returns

Return： 回报，cumulative future reward 即将连续的所有奖励reword求和，得到$U_t$ 表述为如下公式：

\begin{align} U_t = R_t + R_{t+1} + R_{t+2}+ R_{t+3}+... \end{align}

Discounted return： 折扣回报，对于未来的奖励和现在的奖励相比，更倾向于获得当前时刻的回报，并且越久远，奖励就要打折扣，因此对于连续时间下的折扣都有系数，系数为折扣率$\gamma$ ，表示为如下公式：

\begin{align} U_t = R_t + \gamma R_{t+1} + \gamma^{2}R_{t+2}+ \gamma^{3} R_{t+3}+... \end{align}

折扣率$\gamma$ 是一个超参数，是我们可以根据实际情况进行调整的，对强化学习的效果有一定的影响。

回报$U_t$是一个随机函数，随机性有两个来源：

• 执行的动作随机Action can be random

  \begin{align} \mathbb{P}[A=a | S = s] = \pi(a|s). \end{align}

• 场景的新状态随机 New state can be random

  \begin{align} \mathbb{P}[S' = s' | S = s,A =a] = p(s'|s,a). \end{align}

• 对于任意时刻的 $ i \ge t$，奖励$R_i$取决于当前的场景状态$S_i$ 和当前的动作$A_i$

因此，对于$U_t$表示为所有的R求和，即表示$U_t$与未来所有的reward，即未来所有的动作和状态都有关系，这就是折扣回报的随机性来源

Value Functions

State-Value Function

Play games using reinforcement learning

控制AI的两种方式：

第一种，32·

• 提供一个policy函数$\pi(a|s)$

OpenAI Gym