强化学习入门

准备

下面是我搜集的一些学习资料，在之后的学习中，我将继续完善和补充，一起成长！

• 数学基础
  • 高等数学- 宋浩
  • 概率论与数理统计- 孔祥仁
• 理论基础
  • 王树森深度强化学习课程
  • 《强化学习导论》
  • 《神经网络与深度学习》
• 编程基础
  • python基础、面向对象
  • numpy、pandas
  • tkinter、PyQt5
  • 莫烦强化学习
  • Python深度学习
• 综合
  • 动手强化学习 https://hrl.boyuai.com/

个人经验

• 我是在学习了基本的数学知识和python基础之后，看了王树森教授的课程的第一节，对强化学习形成了初步的概念
• 我做了一个PyQt 的python项目，相当于搭建了一个agent的环境，也就是一个地图模拟程序
• 在之后接触了莫烦的教程，从numpy、到pandas，再到强化学习的课程，去实现一个Q-learning的算法，主要还是要项目驱动，如果单纯的无目的学习是很难坚持下去的。

参考文章

• 强化学习中的奇怪概念(一)——On-policy与off-policy

基本知识

• agent 表示动作主体，或者表示执行动作的个体

• state1表示某一状态

• 先看王树森深度强化学习课程 ，第一节

• 再看莫烦强化学习入门课

Q-learning

• 请先看这个莫烦Q-learning课

决策过程

• 存在状态S1，表示一个当前状态
• 存在状态S2，表示做出一个动作之后的新状态
• 存在动作a1,a2，表示两种不同的动作

假设我们已经学习好了行为准则(既对行为的好与坏的评分准则)。根据我学习的经验，将当前状态S1和可执行的动作放入记忆Q_table，交叉表示潜在奖励，其中>0表示当前动作会产生好的结果，相反则表示产生不好的结果，或者进入一种不好的状态。表格如下

状态\动作	action1	action2
state1	-2	1

agent基于根据表格，action2 > action1，因此agent选择动作2

根据上述的动作，我们达到了新的状态S2，形成新的记忆Q表，此时根据我之前选择的经验当前状态对不同动作的奖励值发生了变化，agent始终选择奖励高的选项。因此agent继续选择action2

状态\动作	action1	action2
state2	-4	2

根据第二次动作，我们有到达新的状态S3，依次循环下去，直到agent找到赢得当前规则的状态。

Q表的更新

1. 首先agent根据先验的经验产生一个当前状态S1和动作之间的Q表，并且做出较大值的决策到达新状态S2

   状态\动作	action1	action2
   state1	-2	1
   state2	-4	2

2. 此时agent并不会采取实际行动，而是在想象中(既agent的演算中)判断下一个动作的Q值大,下方的公式表示现实情况下我们的Q值，但是此时的R实际上为0,因为此时并没有行动，公式如下：

   $R$表示到达下一状态后获得的奖励

   $\gamma$ 表示衰减值，通常小于1

   $maxQ(S2)$ 表示在S2状态时，选择奖励较大的那个动作，既Q(s2,a2) = 2。

   \begin{align} Q(s2,a2)reality =R + \gamma * maxQ(S2) \end{align}

   在形成新的Q表之前，我们已经有了一个对下一状态各个动作的估计，即初始Q表，公式如下：

   \begin{align} Q(s2,a2)estimate = 2 \end{align}

3. 根据上述的现实和估计，我们可以算出之间的差距，即 差距(difference) = 现实 - 估计，并将差距放到如下公式中，得出新的Q值：

   $\alpha$表示学习效率，通常也小于1

   \begin{align} Q(s2,a2)(new) = Q(s2,a2)(old) + \alpha * difference \end{align}

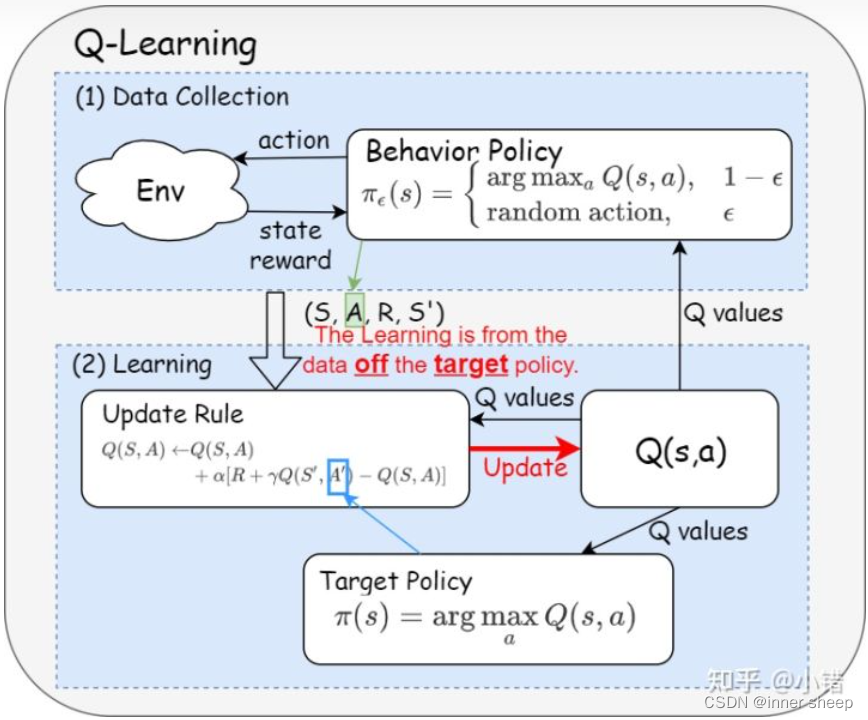
   但此时s2的行为还没有执行，需要等到做出决策后再重新赋值，这是一个off policy的算法，即数据来源于一个单独的用于探索的策略(不是最终要求的策略)。

算法流程

$\epsilon-greedy$ 表示我选择动作时的噪声，即agent有一定几率选择随机的action，通常为0.1

知乎的一个大佬将它分解如下图

案例实现 - o找宝藏

#!/usr/bin/env python3
# -*- coding:utf-8 -*-
import numpy as np
import pandas as pd
import time

np.random.seed(2)  # reproducible

N_STATES = 10  # 表示状态的个数，也就是agent环境中的状态个数，也可理解为地图的尺寸 the length of the 1 dimensional world
ACTIONS = ['left', 'right']  # 表示所有状态下可选择的动作action的种类 available actions
EPSILON = 0.9  # 表示我选择动作时的噪声，即agent有一定几率选择随机的action  greedy police
ALPHA = 0.1  # 学习效率 learning rate
GAMMA = 0.9  # 衰减度，即当前的动作对未来的奖励的影响承度 discount factor
MAX_EPISODES = 13  # 表示学习的次数 maximum episodes
FRESH_TIME = 0.3  # 表示走一步花费的时间 fresh time for one move


def build_q_table(n_states, actions):
    table = pd.DataFrame(
        np.zeros((n_states, len(actions))),  # q_table initial values
        columns=actions,  # actions's name
    )
    # print(table)    # show table
    return table


# print(build_q_table(N_STATES,ACTIONS))
#    left  right
# 0   0.0    0.0
# 1   0.0    0.0
# 2   0.0    0.0
# 3   0.0    0.0
# 4   0.0    0.0
# 5   0.0    0.0
# 6   0.0    0.0
# 7   0.0    0.0
# 8   0.0    0.0
# 9   0.0    0.0

# np.random.uniform 从均匀分布中提取样品。
def choose_action(state, q_table):
    # This is how to choose an action
    state_actions = q_table.iloc[state, :]  # 将当前状态的各个action对应的值赋值给
    if (np.random.uniform() > EPSILON) or ((state_actions == 0).all()):  # act non-greedy or state-action have no value
        action_name = np.random.choice(ACTIONS)
    else:  # act greedy, idxmax 表示取序列中的最大值的动作名称
        action_name = state_actions.idxmax()
        # replace argmax to idxmax as argmax means a different function in newer version of pandas
    return action_name


# 伪随机数生成
# a = np.arange(5)
# print(np.random.choice(a, 5))
# print(np.random.choice(a))


def get_env_feedback(S, A):
    # This is how agent will interact with the environment

    if A == 'right':  # move right
        if S == N_STATES - 2:  # terminate
            S_ = 'terminal'
            R = 1
        else:
            S_ = S + 1
            R = 0
    else:  # move left
        R = 0
        if S == 0:
            S_ = S  # reach the wall
        else:
            S_ = S - 1
    return S_, R  # 返回下一个state和reword


#
# episode回合
# 更新环境函数
def update_env(S, episode, step_counter):
    # This is how environment be updated
    env_list = ['-'] * (N_STATES - 1) + ['T']  # '---------T' our environment
    if S == 'terminal':
        interaction = 'Episode %s: total_steps = %s' % (episode + 1, step_counter)
        print('\r{}'.format(interaction), end='')
        time.sleep(2)
        print('\r                                ', end='')
    else:
        env_list[S] = 'o'
        interaction = ''.join(env_list)
        print('\r{}'.format(interaction), end='')
        time.sleep(FRESH_TIME)


#
def rl():
    # main part of RL loop
    # 创建一个初始化的Q_table,里面都是0
    q_table = build_q_table(N_STATES, ACTIONS)

    # 执行MAX_EPISODES 回合
    for episode in range(MAX_EPISODES):
        step_counter = 0  # 记录所走的步数
        S = 0  # 初始的状态是0
        is_terminated = False  # 是否已经到终点
        # 改变显示的状态
        update_env(S, episode, step_counter)
        # 判断是否结束
        while not is_terminated:
            # 根据当前状态，在Q表中选择一个动作返回给A
            A = choose_action(S, q_table)
            # 选择一个动作执行到达新的状态，并从环境中得到反馈
            S_, R = get_env_feedback(S, A)  # take action & get next state and reward
            # 得到执行动作A之前的状态S对应的动作的Q值(表示先验的，已经在Q表中的，也叫估计值，)
            q_predict = q_table.loc[S, A]

            # 判断新状态是否已经结束，即到达目的地
            if S_ != 'terminal':
                # 得到Q的现实结果
                q_target = R + GAMMA * q_table.iloc[S_, :].max()  # next state is not terminal
            else:
                # 到达目的地，则将奖励值赋给此时的目标Q表
                q_target = R  # next state is terminal
                is_terminated = True  # terminate this episode

            # 总的公式更新Q表
            q_table.loc[S, A] += ALPHA * (q_target - q_predict)  # update
            # 将状态更新
            S = S_  # move to next state

            # 执行更新显示的状态
            update_env(S, episode, step_counter + 1)
            # 走的步数加1
            step_counter += 1
    return q_table


if __name__ == "__main__":
    q_table = rl()
    print('\r\nQ-table:\n')
    print(q_table)

Sarsa

• 与Q-learning算法的决策过程相同，同样使用Q表，但是Q表的更新过程不同
• 请先看这个莫烦Sarsa课

决策过程

• 存在状态S1，表示一个当前状态
• 存在状态S2，表示做出一个动作之后的新状态
• 存在动作a1,a2，表示两种不同的动作

假设根据Q-learning的开始过程，我们已经学习好了行为准则(既对行为的好与坏的评分准则)。根据我学习的经验，将当前状态S1和S2的可执行的动作放入记忆Q_table，交叉表示潜在奖励，其中>0表示当前动作会产生好的结果，相反则表示产生不好的结果，或者进入一种不好的状态。表格如下：

状态\动作	action1	action2
State1	-2	1
State2	-4	2

在Sarsa的决策过程中和Q-learning相同都会选择值较大的那一个action

Q表更新过程

1. 首先agent根据先验的经验产生一个当前状态S1和动作之间的Q表，并且做出较大值的决策到达新状态S2

2. 在状态S2时，估计的动作也就是接下来要做的动作，因此有：

   \begin{align} Q(s2,a2)estimate = 2 \end{align}

   \begin{align} Q(s2,a2)reality =R + \gamma * Q(S2,a2) \end{align}

3. 根据上述的现实和估计，我们可以算出之间的差距，即 差距(difference) = 现实 - 估计，并将差距放到如下公式中，得出新的Q值：

   $\alpha$表示学习效率，通常也小于1

   \begin{align} Q(s2,a2)(new) = Q(s2,a2)(old) + \alpha * difference \end{align}

   因此，Sarsa也叫on-policy算法

算法过程对比

对比Sarsa和Q-learning，可以看出，Sarsa在每一步都根据当前选择的action去更新Q值而不会选择奖励最大的action去更新Q值，这样就会使得Q-learning算法看上去更勇敢。

总结

总体上Q-learning与Sarsa有两个不同：

• Sarsa当前估计的动作，就是我下次执行的动作。Q-learning则不一定是下次执行的动作，会重新选择。
• Sarsa更新Q表基于我当前执行的动作，而Q-learning则选用Q值最大的那个动作

# 算法决策部分的不同
# off-policy
class QLearningTable(RL):
    def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):
        super(QLearningTable, self).__init__(actions, learning_rate, reward_decay, e_greedy)

    def learn(self, s, a, r, s_):
        self.check_state_exist(s_)
        q_predict = self.q_table.loc[s, a]
        if s_ != 'terminal':
            q_target = r + self.gamma * self.q_table.loc[s_, :].max()  # next state is not terminal
        else:
            q_target = r  # next state is terminal
        self.q_table.loc[s, a] += self.lr * (q_target - q_predict)  # update


# on-policy
class SarsaTable(RL):

    def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):
        super(SarsaTable, self).__init__(actions, learning_rate, reward_decay, e_greedy)

    def learn(self, s, a, r, s_, a_):
        self.check_state_exist(s_)
        q_predict = self.q_table.loc[s, a]
        if s_ != 'terminal':
            q_target = r + self.gamma * self.q_table.loc[s_, a_]  # next state is not terminal
        else:
            q_target = r  # next state is terminal
        self.q_table.loc[s, a] += self.lr * (q_target - q_predict)  # update

小项目

• 类似Q-learning的项目略

Sarsa(λ)

什么是Sarsa(λ)？

之前学的Sarsa可以看作是单步更新Q值的算法，即Sarsa(0)，如果我们经过一个回合后拿到奖励才去更新Q值，我们就实现了回合更新,即Sarsa(n)。回合更新使得我只有在找到目标获得奖励后，才将之前的跟获得奖励有关的所有步更新，这样就好了嘛？

并不是，如果我们在某个角落多次徘徊的话，我们就会使得这个角落的所有Q值都得到更新，这显然容易让Agent陷入一个死角，因此我们需要一个衰减值λ。

站在获得奖励时的状态往回看，离我获得奖励越远的动作action，就对我获得奖励的价值相对减弱，这个损失值就为λ，这样我就会使得更容易获得奖励的action得到更高的Q值更新，从而使得agent趋向于获得奖励。

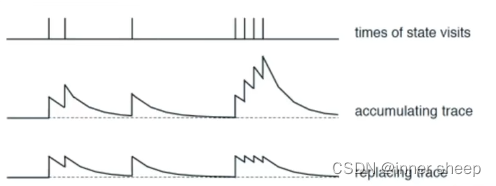
损失过程

• 第一行表示在一个时间轴上我遇到奖励的时间
• 第二行表示第一种方法，我只要遇到了奖励我就对当前所有经过的路径更新Q值，但是可能出现超高的Q值这样会对我的决策产生影响
• 第三行表示第二种方法，为了避免上一种方法的情况发生，我设置一个阈值，这样就不会有超高Q值的情况出现，使得学习效果更好。

算法过程

DQN

• 对于复杂的问题，传统的表格已经不能满足程序的性能，因此需要神经网络生成Q值，这样就不需要记录Q表

什么是DQN？

• 将状态和动作输入神经网络，让神经网络产生Q值
• 或者只输入状态，让神经网络产生不同动作的Q值，再用Q-learning的方法选择动作

  • 强化学习中神经网络如何被训练

安装OpenAI gym